Fundamental Magnetism

Fundamental Magnetism

Apr 02,2021

Fundamental Magnetism

1. Q: What is Magnetic Field Strength?

A: Magnetic field is a physical phenomena induced by the motive electric charges in their surrounding space. Magnetism of materials arises from two atomic sources: the spin and orbital motions of electrons. Therefore, the magnetic characteristics of a material may change as a function of alloying constitution. Magnetic field strength is the measure of the vector magnetic current, or a magnetic body, to induce a magnetic field at a given point, denoted as H, measured in A/m (amperes per/meter, SI electromagnetic unit system) or Oe (oersteds, CGS electromagnetic unit system). One unit of A/m is defined as the field strength value induced by an infinite long linear conductor bearing one unity ampere electric current that locates 1/(2Л) meters away from the measured position. 1Oe=1/(4Л)×10³A/m.

 

2. Q: What is the Relationship between Magnetic Induction, what is Field Strength and Polarization Strength?

A: Magnetic induction is the magnetic field induced in a medium by a magnetic field strength at a given point, denoted as B, measured in gauss (Gs, CGS unit) or teslas (T, SI unit), 1T=10⁴ Gs. It is the vector sum, at each point within the medium, of the magnetic field strength and resultant polarization strength. Magnetic induction is also defined as the number of flux line per unit area normal to the direction of the magnetic path. Magnetic polarization strength is also called intrinsic induction, denoted as J, measured in gauss or teslas. It is the vector sum of the magnetic dipole moments of a unit material. It indicates the vector difference between the magnetic induction in the material and the magnetic field strength. This relation is expressed by the following equations:

   B=µ₀H +J    (SI)               (1-1)

   B=H+4ЛM   (CGS)             (1-1a)

µ₀ is the magnetic permeability in vacuum. In CGS unit,

µ₀ =1Gs/Oe, while is SI unit, µ₀ =4π×10⁷Wb.A^ˉ1.M’^-1. (webers per ampere and meter).M is known as magnetization, similar as polarization J, representing the vector sum of individual  atomic magnetic moments per unit volume, and there has J=µ₀M.

 

3. Q: What is Magnetic Flux?

A: Magnetic flux is a contrived but measurable concept that has evolved in an attempt to describe the “flow” of a magnetic field. It was creatively proposed by Michael Faraday (1791-1867).The unit of magnetic flux is maxwell in CGS unit. One maxwell is defined as one of magnetic flux that is perpendicularly passing through a section area of one square centimeter. In SI unit, the unit of magnetic flux is weber (Wb), 1Wb=10⁸ maxwells.

Flux is mathematically described as the surface integral of the normal component of the induction B over an area S:

φ=

When the magnetic induction is uniformly distributed and is normal to the area, the flux in maxwells is:

φ= BS                    (1-2a)

Where B is the magnetic induction in gauss, and S is an element of area in square centimeters. Thus, the unit of induction B and polarization J can also be expressed as Wb/m² or maxwell/cm²: 1 T=1 Wb/cm², and 1Gs=1 maxwell/cm².

One of the most important characteristics of the magnetic flux is that flux must always be conserved in any complete magnetic circuit. This means that for any closed region that is within must equal to the total flux that enters into it, flux must be conserved through any region. That is, any flux line must be complete loops. This is one of the two fundamental principles that form the basis for magnetic circuit design (refer to Q4-3).

 

4. Q: What are the Principal Properties of a Permanent Magnet?

A: Permanent magnets are identified by the following principal magnetic properties:

Maximum value of energy products (BH)_m, in unit of MGOe(megagauss-oersteds, CGS unit) or J/m³(joules per cubic meter, SI unit),4Π×10KJ/M3=1 MGOe;

Residual induction B_r, in unit of Gs or T;

Coercive force H_cb, in unit of Oe or A/m;

Intrinsic coercive force H_cj, in unit of Oe or A/m;

The measurement of the principal magnetic properties is made in a closed magnetic circuit tester by commonly accepted procedures. The minimum magnet volume of a sample used to measure these magnet properties shall be one cubic centimeter and the smallest dimension shall be at least 5 mm. The performance of a permanent magnet circuit depends on the dimensions and the properties of all the components of the circuit.

 

5. Q: How to distinguish the Permanent Magnetic (Magnetically Hard) Material?

A: A permanent magnet material, also designated as a magnetically hard material, has a coercive force generally greater than 120 Oe. Otherwise, the magnetic material is defined as magnetically soft material. Currently used permanent magnets include Alnico, hard ferrite, Sm-Co, Nd-Fe-B etc. Among these magnets, sintered Nd-Fe-B has the strongest permanent magnetic properties. Frequently used soft magnetic materials include pure iron, low carbon steel, soft ferrite, silicon steel, Ni-Fe alloy etc.

Permanent magnet and soft magnetic material can be distinguished by the following characteristic. Insert the materials into a strong magnetic field and magnetize it to saturation, then remove it from the field, A permanent magnet will continue to exhibit a magnetic field while the soft magnetic material has practically no appearance field. This disparity is originated form the difference of the coervice force of the materials (refer to 1-8 and 1-9 Q).

 

5. Q:What is the Polarity of a Magnetized Magnet?

A: The North Pole of a magnetized magnet is that pole which is attracted to the geographic North Pole. The North Pole of a magnet will repel the North Pole of a magnetic compass. Apparently, the geographic North Pole is essentially the magnetic South Pole. Therefore, the magnetism of the Earth can be analogized as a huge “permanent magnet” which locates at the center of the Earth. The magnetic North Pole of this “permanent magnet” points to the geographic South Pole and its magnetic South Pole to the geographic North Pole.

The polarity of any single magnet is always appeared as N-S(North-South) dipole. That is, magnetic monopole is impossible in the world, all magnetic North Poles must be paired with comparable South Poles.

The magnetic flux line is designated as starting from the North Pole and entering into South Pole.

 

7. Q:What is the Residual Induction of a Permanent Magnet?

A: The residual induction is any magnetic induction that remains in a magnetic material after removal of an applied saturating magnetic field, measured in gauss or teslas, denoted as B_r or J_r. Residual induction is also known as magnetic ramanence.

From equation (1-1) we know, when H=0, B_r = J_r. For rare earth permanent magnets such as Sm-Co and Nd-Fe-B, with the increasing of the reverse applied field H, the magnetic induction B decreases linearly in any value of J or B on the second quadrant of demagnetization curve of J or B on the second quadrant of demagnetization curve must be less than B_r or J_r. This can also be comprehended as the material intrinsic magnetic polarization J cannot increase along with the inversely increased magnetizing force H.

 

8. Q:What is the Coercive Force of a Permanent Magnet?

A: The coercive force of a permanent magnet is equal to the demagnetizing force required to reduce the residual induction to zero in a magnetic field after magnetizing to saturation, measured in oersteds or A/m, denoted as H_c or H_cb. That is, when the external applied demagnetizing field exactly reaches H_cb, the magnet has no apparent magnetic flux any more.

Equation (1-1) indicates, when H=H_cb, B=0 and J=-μ₀ H_cb. As any value of J or B on the second quadrant of demagnetization curve must be less than B_r or J_r, μ₀ H_cb must thus be small than B_r or J_r in absolute value. For example, when a permanent magnet has a remanence B_r=12.3 kGs then its coercive force H_cb cannot be greater than 12.3 kOe.

 

9. Q:What is the Intrinsic Coercive Force of a Permanent Magnet?

A: The intrinsic coercive force of a magnetic material indicates its resistance to demagnetization. It is equal to the demagnetizing force, which reduces the magnetic polarization in the material to zero after the magnet is magnetized to saturation, measured in oersteds or A/m, denoted as H_cj.

From equation (1-1) we know, when H= H_cb, B=0 but J is not zero. That is, the vector sum of the magnetic dipole moments in the material is not zero, and the magnet is not totally demagnetized. When the demagnetizing force is removed at this time, the apparent magnetic induction of the magnet will spontaneously regain. So we designate H_cj as the intrinsic coercive force to distinguish it form the coercive force H_cb. It is only when the demagnetizing force reaches up to H_cj, the magnet is totally demagnetized.

 

10. Q:What is the energy product of a permanent magnet?

A: The energy product indicates the energy that a magnetic material can supply to an external magnetic circuit when operation at any point on its demagnetization curve, measured in MGOe or j/m³. The product of magnetic induction B_d for ordinates and magnetic field H_d for abscissa is defined as energy product and denoted as (B_dH_d). The energy product of a permanent magnet (BH)_m that can be obtained on the demagnetization curve (refer to 1-11 Q).

As discussed in 1-8Q, Br≥µ₀Hcb, we can intuitively known that the maximum product (BH)_m must be smaller than Br²/4.

 

11. Q:What is the demagnetization curve of a permanent magnet?

A: For ferromagnetic materials, the response of magnetic induction B to magnetic field H is usually hysteretic. By plotting B against H (usually in rectangular coordinates) close loop. There are infinite hysteresis loops for a permanent magnet according to the magnitude of the external applied fields. Generally, we designate the possibly maximum hysteresis loop as the major hysteresis loop of a permanent magnet. Fig.1-1a shows the typical major hysteresis loops of the sintered Nd-Fe-B permanent magnet. The relationship of B-H is known as the normal curve, and that of J-H is known as the intrinsic curve, the two curves are related at every point by the equation (1-1). That is, we can derive one from the other by equation (1-1).

The demagnetization curve is the second (or equally the fourth) quadrant of a major hysteresis loop. The demagnetization curves for the typical Nd-Fe-B magnet are shown in Fg.1-1b, and there are also two demagnetization curves at the same time, one is B-H, the other is J-H.

The B-H curve is used for magnetic circuit design since it represents the net output of the magnet when it is used to establish energy in an air gap. When the magnet is placed in an external field, the intrinsic curve J-H is used to determine how the external field changes the intrinsic properties. When a permanent magnet reacts with an external field, the intrinsic polarization gives the force or torque on the magnet, because the force results from the interaction between the polarization and the external field.

The operating point of a permanent magnet is a point on B-H demagnetization curve defined by the coordinates (H_d, B_d), point D for example, is shown in Fig.1-1c.The operating line for a given permanent magnet circuit is a straight line passing through the origin and the operating point D of the B-H demagnetization curve with a slope of negative B_d/H_d, line O-P for example, as shown in Fig, 1c. The ratio of magnetic induction to a demagnetizing force B_d/H_d is also known as magnetic permanence coefficient of the magnet or circuit, the operating line is also called permanence coefficient line.

B-J

(a)

(b)B P D B_d-H  Hcb  H_d   O

(c)Fig .1-1 typical hysteresis loops (a) and demagnetization curves (b) of a permanent magnet, the operation point and operation line of a permanent magnet are illustrated in (c)

12. Q: What is the recoil Permeability of a permanent Magnet?

A: Recoil permeability if a permanent magnet is the dynamic slope of the B-H demagnification Curve, demoted as µ_rec, it indicated the characteristics of dynamic minor demagnetizing ands regaining behavior of the magnet, the smaller the value of µ_rec, the higher the stability of the magnet in dynamic operation condition behaves. Generally speaking, the B-H demagnetization curve of sintered Nd-Fe-B, magnet is nearly a straight line, and µ_rec is the average slope of the B-H demagnetization curve, with a constant of 1.03 –1.10. That is, we can approximately express the relationship of B-H as:

                           B = µ ₀H +Br               (1-3)

Recoil permeability µ_rec also represent the queerness of B-H demagnetization curve, the smaller the value of µ_rec, the higher the square ness of B-H demagnetization curve. For B-H demagnetization curve, the ratio of H_k /H_cj, is designated as the square ness, where H_k is defined as the demagnetizing force when J =0.9 J_r..

 

13. Q: What is the Self-demagnetization Field of a Permanent Magnet?

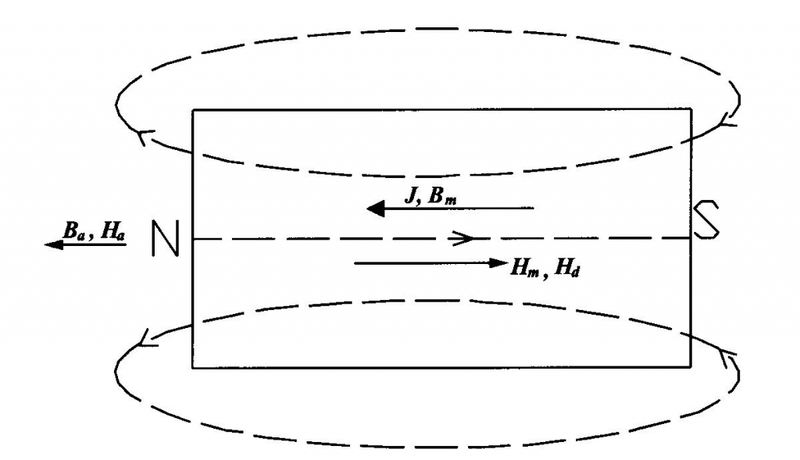
A: Knowing from 1-6Q, the magnetic flux lines are always stating from the North Pole of a magnet, passing through its surrounding medium, and entering into the South Pole. This is the same within the internal region of the permanent magnet, thus, as illustrated in Fig .1-2. Within the permanent magnet, an internal magnetic field H_d, with direction opposite it that of magnetic polarization or formed. As such an internal field H_d has a demagnetizing effect to polarization J of the permanent magnet, we call it as self-demagnetizing field.

The origination of self-demagnetizing field can also be comprehended by magnetism reasoning. Considering the boundary region near the North pole of a permanent magnet as illustrated in fig.1-2, we use B_m, H_m denote the magnetic induction and field within the magnet, and B_a, H_a denote those outside the magnet, that is, in air, knowing from equation (1-1) we have:

                 B_m = µ₀H_m+J, and B_a=µ₀H_a      (1-4)

We have discussed in 1-3 Q that flux must be continuous anywhere. So, within the boundary region considered, there is:       

Fig 1-2：illustration of the origination of self –demagnetization field.

          B_m= B_a, and then H_m= H_a –J/µ₀   (1-4a)

Apart from the boundary region, we intuitively know that:  

          B_m >B_a, thus H_m> H_a-J/µ₀         (1-4b)

Within the permanent magnet, H_a is zero. To eliminate the inequality of (1-4b), we introduce a parameter of 0< n<1. That is:

                    H_d= (-N/µ₀)J       (1-5)

Where we designate H_d= H_m, as it is the only magnetic field exists within the permanent magnet, N is the simply a number known as the demagnetizing factor, depending on the shape of a magnet, and H_d is its self –demagnetizing field, For extremely wide planar magnet, the thickness of the magnet can be taken as near zero, equation (1–4a) clearly indicators that N =1, and equation (1-4) indicated that B_m=0, That is, the magnet shows no appetent flux anymore. While along the axis of a very long needle –hasped magnet, N tends to vet zero, and no self- demagnetizing field exists within the magnet. Demagnetizing factor is only related to geometry, not to physical properties of the magnet.

We should bear the concept on mind that no matter the magnetic magnetically soft or hard the exists self-demagnetizing field during magnetizing force required to saturate a magnet or circuit is the difference of applied field to its self-demagnetizing field, the thinner the magnet, the higher the self-demagnetizing field, and therefore the higher applied field is required

 

14. Q: How to Determine the Demagnetizing Factor and the Operation Point ofPermanent Magnet?

A: As it is discussed in 1-13Q, self-demagnetizing field is the only magnetic field exists within a permanent magnet when there is no external field. Thus, it is the origination of a permanent magnet to produce magnetic induction for circuit. If there is no self–demagnetizing field in magnet such as in strictly closed circuit, the magnet will contribute no energy to outside. Therefore, it is very important to decide the self -demagnetizing field of a permanent magnet for circuit design.

Unfortunately, it is very difficult to calculate the demagnetizing factor of a magnet with a simply formula. Even for magnet with simple’s shapes such as cube and cylinder. Because the flux distribution within the these magnets is not uniform, that is, the demagnetizing factor is the function of position, and does not change linearly with the geometric position in the magnet, it is only ellipsoidal–shaped magnetic material has the unique ability to sustain uniform field along either its major or minor axis (of course, a sphere is a particular case of ellipsoid) so far, only the demagnetizing factor of ellipsoidal–shaped magnet can be calculate with simple formula, for other shaped magnet, the calculation of demagnetizing factor  must  be  recurred to Finite Element Method (FEM) with computer by dividing the total geometry of the magnet into many minor simple regions there in all physical propertied are assumed   to be uniform (4-7Q). As cylinder is one of the most practically useful shaped for magnet, people have measured the relationship of its demagnetizing factors with the ratio of the length of a magnet to its diameter by experiment, as show in FIG.1-3.

Given the demagnetizing factors of a permanent magnet easy to decide to the operating point and operating line of a magnet, by substituting equation (1-5) into equitation (1-1), we get:    

                           B_d=(1-1/N)µ₀H_d      (1-6)

According to the definition in 1-11Q operating point and operating line can be conveniently decided (refer to Fig .1-1C) .For examples, a cylindrical sintered Nd-Fe-B magnet with diameter of 12.5mm, assuming there are no yoke irons, what will be is length so that the magnet can be operated near its maximum energy product? In Fig.1-1 C, assuming H_cb and B_r of the magnet are equal in absolute values, we know that the product of (B_dH_d) is Maximum energy when the operating line O-p has an angle of 45degrees to the coordinate axis. This means the slope of operation lolling O-P is –1.0, and thus, N= 0.5, according to equation (1-6). From Fig 1-3 we know, the ratio, of length to diameter of the magnet L/ D is 0.47 when N=0.5, that is when the length of the cylindrical magnet is 5.88 mm, it can be operated near its maximum energy product.

         Fig.1-3: Relationship of demagnetizing factors N to the ratio of length to diameter L/d for cylindrical, magnet (measured by experiment)

            

15. Q:What are the thermal Properties of a permanent Magnet?

A: The thermal properties of a Permanent are the production magnetic performance as a function of the temperature of the magnet; it requires knowledge of the following thermal propertied:

Reversible temperature coefficient if the residual induction, α_Br (%/ºC);

Reversible temperature coefficient of the intense coercive force β_Hcj (%/ºC);

Curie temperature, T_C (%/ºC);

Maximum operable temperature, T_w (%/ºC)

The reversible temperature coefficient is a factor that describes the reversible change of magnetic property with a change in temperature. The magnetic property spontaneously returns when temperature is cycled, to its original point, it is usually express the as percentage change per unit temperature. The reversible temperature coefficient is related to the basic chemical contents and microstructure of the material.

For every kind of ferromagnetic material, there exists a transition temperature above which the material loses its ferromagnetic properties, defined as Curie temperature cure T_c. As shown in Fig, 1-4, with the increasing of temperature, the polarization strength J of a magnetic material decrease due to the thermal agitation of dipole moments in material. Once the temperature exceeds T_c, the ferromagnetic material turns to be a paramagnetic. The Curie temperature is one of the intrinsic properties of a magnetic material. It is only related to the alloy contents of the material, not to microstructures.

The maximum is operable temperature T_W, is the maximum temperature to which the magnet may be exposed without significant long-range instability or structural changes, as it is illustrated in Fig 4. T_w is the defined by the “NORMAL OPERARING RANGE”, which is specified by the user and the magnet device requirements, T_w is related to T_c, as well as the temperature coefficient of a permanent magnet because Br and H_cj also change with temperature, Moreover T_w depend on geometry and circuit in which the magnets use due to irreversible losses consideration.

Fig. 1-4: Relationship of magnetic polarization to temperature of ferromagnetic material.

16. Q: What are Irreversible Losses of a Permanent Magnet?

A: The irreversible losses of a permanent magnet are defined as partial of the magnet, caused by exposure to high or low temperatures, external fields or other factors. These losses are recoverable by re-magnetizing unless the chemical composition or the metallurgic structure changes, Magnet can be stabilized against irreversible losses of a permanent magnet depend on the microstructures of the material as well as geometry and circuit in which the magnet is used Generally, irreversible looses of a permanent magnet increase when the length along magnetizing direction, decreases for the reason of self-demagnetizing effect.

 

17. Q: What is Magnetic Domain?

A: The concept of magnetic domain was proposed by French physicist Pierre Weiss in 1907 to interpret the microscopic behavior of ferromagnetic materials, Weiss1s theorem possesses postulated that a ferromagnetic body must be composed of some regions or domain each of which possesses a magnetic saturation level, but the direction of the magnetization from the domain to domain need not to be parallel, when a magnet is demagnetized, it is only demagnetized from the viewpoint of an observer outside the

Fig. 1-5: The typical magnetic domain pattern of sintered Nd-Fe-B magnet measured by MFM.

material. External field only serve as control in changing the balance of potential energy within a magnet, this theorem still provide the basis of our highly sophisticated body of knowledge that explains quite satisfactorily the observed properties of ferromagnetic material and provides, an intelligent guide for the search for improved, material magnetic domain is constituted by domain body and domain walls, it is the physical phenomenon essentially derived from the balance of various micro and macro energies of the ferromagnetic material, thus  domain sizes vary widely with composition, purity and state of internal  stress as well as some internal external energy of the material, modern permanent magnets exhibit intrinsic coercive forced well above the level explained by the domain wall motion theory founded in the age of Weiss. A significant milestone in understanding permanent magnet properties occurred with the suggestion of E.C stoners and E.P. Wohlfarth that, if small particles were prepared with dimensions less than the width of a domain boundary, such particles would contain no domain walls. This explanation forms the central concept in fine particle magnet theory and provides a satisfactory explanation of modern high coercive force magnets such as Alnico, hard ferrite, rare earth cobalt and rare earth iron magnets.

Magnetic domain is the unique microstructure of magnetic materials. Almost all of the microscopic behaviors of ferromagnetic materials are related to domain.

               (c)       (d)

Figure 1-6: The basic behavior of the magnetic domain in a crystal grain of

 the magnet during magnetizing. (a) The external field H=0; from

 (b)to (d), the external applied field increases gradually.

Magnetic domain can be observed by using Bitter Pattern, Faraday Polariscope or magnetic Force Microscope (MFM). Figure 1-5 is the typical magnetic domain pattern of sintered Nd-Fe-B magnet measured by using MFM. There are multiple lath-like domains within the crystal grains in which the magnetization vector (magnetic polarization) is approximately parallel to the orientation direction of the magnet. The “black” region in Fig. 1-5 is a misalignment grain whose easy axis greatly departs from the orientation direction of the magnet.

Figure 1-6 illustrates the basic behavior of the magnetic domain in a crystal grain of the magnet during magnetizing. Here, the small arrows represent the polarization direction of each magnetic domain, and the black arrow represents the direction of the external applied magnetizing field. Figure 1-6a shows the magnetic domain pattern in thermal demagnetization state when the applied field is zero. When the magnetizing field is applied, the domain walls will be driven to move as illustrated in Fig. 1-6b. The motive behavior of the domain walls must satisfy the principle of minimum static magnetic energy, that is, those domain whose polarization vector direction are closer to that of the external field will annex their neighbors. With the increase of the applied field, as the illustrated in Fig. 1-6c, the entire crystal grain will become a single domain. Once the applied field increases further, as shown in Fig. 1-6d, the magnetization vector of the grain will rotate gradually to the direction of the applied field, herein, the magnet is magnetized to saturation.

For demagnetizing process of permanent magnets, the behavior of the magnetic domain is similar. Wherein, the demagnetizing curve is determined by the formation of the domains whose polarization vector direction is reverse to the orientation direction of the magnet. These reverse domains are usually formed in the boundary region of the grains or in that of the defects in the crystal grains. The formation of the reverse domains is basically determined by the alloying composition and microstructure of the material. The harder the formation of the reverse domains is, the greater the coercive force of the magnet is.

18. Q: Why are there so many Scientist Names Appearedin Electromagnetic Unit System? What are their Stories?

A: The naissance and development of magnet is a far-flung way. Looking back the history of human being, the advancement of magnet is essentially appeared as sounding a little tone of romanza. Nevertheless, during the past 200 years, the great achievements of human being on magnetism are greatly amazing.

In about 2600 years ago, the Greek firstly investigated the natural magnet-lodestone. It is said that the word “magnet” is derived from Magnesia, a Greek district where lodestones are found. In 480-221 B. C., the Chinese created for the first time the magnetic compass-the first practical magnetic device. The word “磁石” meaning magnet is said also from a district name-Ci county, Hebei province, China – where lodestones were mined. After that, it had taken almost 2400 years before the human actually established magnetism.

In 1600, William Gilbert, the personal physician to Queen Elizabeth I, published his volume, De Magnet, symbolizing the initial investigation on electromagnetism. Gilbert is honored today by use of the term gilbert as the unit of magnetomotive force.

On July 21, 1820, Hans Christian Oersted published his epochal discovery. 2400 years after the Greek, the connection between magnetism and electricity had been fused; electromagnetism was born. We use today the term oersted as the unit of magnetic field strength in honor of Oested. After a few days of Oersted’s discovery in 1820, Andrè Ampère propounded the law of electromagnetism (Ampère’s law) that describes mathematically the relationship between magnetic field and electric current. Importantly, Ampere stated out in a creative way that the magnetism of matter is essentially originated from the micro atomic current in the matter. Wilhelm Eduard Weber (1804-1891), a German physicist, who with his friend Karl Friedrich Gauss (1777-1855), the greatest mathematicians of all time, investigated terrestrial magnetism. Weber’s work on the ratio between the electrodynamic and electrostatic units was crucial to Maxwell’s electromagnetic theory. Weber and Gauss are honored today by use of the term weber and gauss, as the unit of magnetic flux and flux density respectively.

James Clerk Maxwell (1831-1879) is ranked with Newton and Einstein for the fundamental nature of his many contributions to physics. Most importantly, he originated the concept of electromagnetic radiation and his field equations. We today use the term Maxwell as the unit of magnetic flux in honor of Maxwell. Maxwell’s equations agglomerate the wisdom of a lineup of brilliant men from 1820 to 1860, who established practically all of the familiar electric and magnetic laws. The names include: Ampere, Biot, Coulomb, Faraday, Gauss, Green, Helmholtz, Henry, Joule, Kirchoff, Lenz, Kelvin, Maxwell, Ohm, Poisson, Savart and Weber. Nikola Tesla (1856-1943) held more than 700 patents. His inventions included the principle of the rotating magnetic field machine, the induction motor, polyphase alternating-current systems, the Tesla coil transformer, wireless communication, radio, and fluorescent lights. Today, the term tesla is used as the unit of magnetic polarization in honor of Tesla.

 

19. Q: What is the History of Permanent Magnets?

A: Lodestones had dominated the human’s permanent magnet for thousands of years, whose magnetic residual induction and coercive force is less than 4000 Gs and 200 Oe respectively. Nevertheless, the coercive force of the nature permanent magnet was not surpassed by man-made magnets until the twentieth century.

The first man-made permanent magnet is carbon steel developed in eighteenth-century in England. After that, alloying elements were adopted to increase the coercive force of carbon steel, and the best alloy steel with maximum energy product of 1 MGOe was finally developed in the 1920s.

In 1932, Japanese metallurgist Dr. Tokushichi Mishima of Tokyo University developed a new alloy magnet called MK steel (Fe-Al-Ni), which had the highest coercive force up until then; i.e. 300-600 Oe. MK steel was soon improved by additions of cobalt and other elements and “Alnico” magnets began to replace steel magnets in numerous applications.

Although Alnico magnets have excellent residual induction (up to 14000Gs) and maximum energy product (up to 13 MGOe), their coercive force (less than 2000 Oe) cannot yet fully meet the growing needs of electrical industry for the reason of easy demagnetizing. In 1960s, barium and strontium ferrite magnets called hard ferrite were developed by Philips in The Netherlands. Hard ferrite has much higher coercive force (greater than 2000Oe) and much lower cost than Alnico magnets, and led to their widespread use in many applications since 1960s. Today, hard ferrite magnets continue to dominate the permanent magnet market, so we remain in the “ferrite age”.

In March 1967, the Journal of Applied Physics published an article by American physicist Karl Strnat and his colleagues entitled “ A Family of new Cobalt-Base Permanent Magnet Materials”, and symbolizing the naissance of a new generation of permanent magnet – rare earth permanent magnet. The firstly developed rare earth magnet is SmCo₅, an intermetallic compound constitutes of samarium and cobalt in atomic ratio of 1:5. SmCo₅ magnets possess maximum energy product up to 24 MGOe and intrinsic coercivity up to 30kOe or even higher. In 1976, Karl Strnat and Zyoshio Tawara created the “second generation” of rare earth magnet Sm₂Co₁₇, whose maximum energy product reaches up to 32 MGOe.

In 1983, the “third generation” rare earth permanent magnets based on Nd₂Fe₁₄B were developed simultaneously in Japan and U.S.A. The magnet developed in Japan was made by power metallurgic process: by making the alloy powders, then pressing and sintering into bulk magnets. While the fabricating method developed in U.S.A. was a melt-spinning process: by manufacturing the microcrystal alloys, then making powders, and followed by hot pressing or polymer bonding to fabricate the bulk magnets. Nd-Fe-B magnet is the strongest man-made permanent magnet so far. Today, Nd-Fe-B magnets with maximum energy product greater than 50MGOe, these Nd-Fe-B magnets are in mass manufacturing. In merits of much cheaper raw materials and higher energy product than those of Sm-Co magnets, the production scale of Nd-Fe-B magnets has been growing year by year.